sin^3 x + cos^3 x = cos 2x
I meet some problems in solving some equations. I tried a lot of methods, but I didn't get any solution, so I'd be grateful if you could give some ideas.
1)  , for
, for 
At first, I tried to write
(\sin^2 x + \cos^2 x - \sin x \cos x))
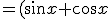(1- \sin x \cos x))
but I don't know how to solve next.
Then, I wrote 
If  = 0)

^(k+1) arcsin 1 + k \pi = (-1)^(k+1) \frac{\pi}{2} + k \pi, k \epsilon Z )
If \cos x \neq 0 \Rightarrow \frac{\sin^3 x}{\cos^3 x} + \frac{\cos^3 }{\cos^3 x} - \frac{\cos^2 x}{\cos^3 x} + \frac{\sin^2 x}{\cos^3 x} = 0 \Rightarrow \tan^3 x + 1 - \frac{1}{\cos x} + \tan^2 \frac{1}{cos x} = 0 \Rightarrow \tan^3 x + 1 - \frac{1}{cos x} (\tan^2 x - 1) = 0 \Rightarrow (\tan x + 1)(\tan^2 x - \tan x + 1) - \frac{1}{\cos x} (\tan x -1)(\tan x + 1) = 0 \Rightarrow (\tan x +1)[\tan^2 x - \tan x +1 - \frac{1}{\cos x}(\tan x -1)] = 0 \Rightarrow (\tan x +1)[\tan x (\tan x -1) + 1 - \frac{1}{\cos x}(\tan x - 1)] = 0 \Rightarrow (\tan x +1)[(\tan x -1)(\tan x - \frac{1}{\cos x})+1] =0 \Rightarrow (\tan^2 -1)(\tan x - \frac{1}{\cos x} + \tan x + 1) = 0 \Rightarrow (\tan^x -1)(2 \tan x - frac{1}{\cos x} + 1) = 0[/math]



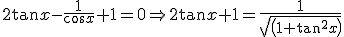} \Rightarrow (2 \tan x + 1)^2 = \frac{1}{1 + \tan^2 x} \Rightarrow (1 + \tan^2 x)(2 \tan x +1)^2 = 1)
Is this correct? If it is, how to solve next?
2)  = 4)


^2 + 4 \tan^2 x - 4 \tan x (\tan^2 x -1) = 0)
What to do now to get the solution?
Thank you for taking time to read this.
, for
